|
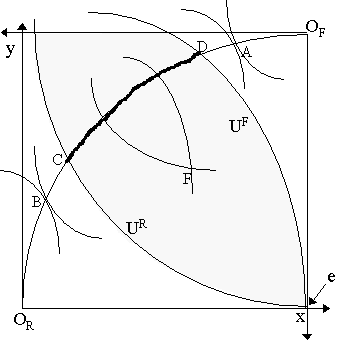
Anthropologists tell us that 150 is about the maximum number of people any given individual can know intimately enough to bond with. We know that in Edgeworthian exchange, agents who are in the process of forming coalitions must know the preferences and endowments of others. If we decide to call this "intimacy" and call coalitions "bonding", then what are the consequences of the anthropologists' observation for the theory of the core? It is clear that the process of coalition-formation is going to be restricted, but exactly in what manner? There are two meanings we can attach to their observation. The first interprets the restriction on the "intimacy" part. In this case, the coalition-formation process is dominated by incomplete information. In other words, in an economy with H people, a person will only know the preferences and endowments of a subset K Ì H of people and can only form coalitions with people from this group. There is an upper maximum to the size of possible coalitions in the economy. A second interpretation places the restriction on the "bonding" part. In other words, even if the person knows all H people "intimately" (knows their endowment and preferences), he does not know them well enough to "bond" with (i.e. form coalitions). In other words, if he wishes to form a coalition, he only form one with a maximum of 150 people -- albeit, anybody can be contained in this 150. It is this type of restriction that we shall consider here. [Note: another interpretation of the second type of restriction is that there are "transactions costs" to coalition-formation. But that would be a less colorful interpretation.] What are the consequences of placing an upper limit on the size of possible coalitions? Intuitively, the "core" will be larger. To see this, examine Figure 1, where we have a simple two-person (Robinson, Friday), two commodity (x, y) economy. The regular core is represented by the segment of the contract curve between the two autarky indifference curves, namely the thick line stretching from C to D in Figure 1. We know this will be the case because any other allocation will be blocked either by (a coalition of) one or both of the agents. For instance, any allocation below Robinson's autarky indifference curve UR (e.g. B) will be blocked by Robinson; similarly, Friday will block any point above UF (e.g. A). Points inside the shaded lens that are nonetheless off the contract curve (e.g. allocation F) cannot be blocked by either agent, but can be blocked by both together. Thus the set of core allocations will be strictly the contract curve segment between C and D.
Consider now what happens when we restrict the size of coalition formation, i.e. place a maximum on the number of people that can participate in one. We can use the counting measure, m = #S/#H (the proportion of all people in the economy H that are in the coalition S) for this. If the maximum is m (S) = 1, then coalitions can be of any size -- and thus the core will be our regular core (e.g. between C and D in Figure 1). If m (S) = 3/4, then this implies that a coalition cannot exceed three-quarters of the people in the economy. In the Robinson-Friday economy, then each person is half of the economy. In this case, the restriction m (S) = 3/4 implies that a coalition cannot be composed of both Robinson and Friday. As the maximum coalition can be only contain one person, then points like F can no longer be blocked (although A and B still can). Thus, the core is now "enlargened" to the entire shaded lens in Figure 1. If the maximum m (S) = 1/4 then a coalition cannot exceed 1/4 of the people in the economy. In the Robinson-Friday case, each person is a half, thus we have effectively outlawed all coalitions composed of one or two persons. Points such as A and B can no longer be blocked. The resulting core will been enlarged to the entire Edgeworth-Bowley box in Figure 1. We call a core with an upper maximum a "restricted core" or "e -core" (read: epsilon-core). Formerly, let us define e -blocking (read: "epsilon-blocking") as:
Thus, an allocation x is called "e -unblockable" if there is no coalition S of size 0 < m (S) £ e and alternative allocation that can block x. So, we can now define the e -core:
In finite economies, as we saw in our simple Robinson-Friday economy, restricting the size of possible coalitions enlarges the core. Thus, in general, we can claim that for any restriction e , the e -core is larger than the core, formally:
Proof: C(E) = Ç e (Ce (E)) for all e Î [0, 1], i.e. the core can be constructed by taking the intersection of all possible e -cores. § Now for something surprising: in an atomless (and thus continuum) economy, the e -core is not larger than the core. Indeed, whatever e is, Ce (E) is identical to C(E). This surprising equivalence result was first proposed and proved by David Schmeidler (1972). We follow him here:
Proof: Schmeidler (1972). We have shown that C(E) Ì Ce (E). So, all that remains is to show that C(E) É Ce (E). All we need to show is that x Ï C(E) implies that x Ï Ce (E). Suppose then that x Ï C(E), then there is an allocation y and coalition S such that y(h) >h x(h) a.e. h Î S and ò S y(h) £ ò S e(h). Now, all we have to show is that this implies that there some other coalition (call it E), which is a subset of S, which also blocks x with allocation y, but which has measure m (E) £ e . To prove this, consider constructing a smaller measure space (S, Á S, l ), where S is the original coalition, Á S is a s -algebra on it and l a measure. We construct Á S by taking the intersections of all sets in Á with S, i.e. for all A Î Á , A Ç S Î Á S. (prove to yourself that the resulting Á S is a s -algebra). For our measure l , we take the following:
for B Î Á S. This is a vector-valued measure over Á S -- where for the first component (actually, first n components, as we have n goods) we use the integral of [y(h) - e(h)] over the set as measure; for the second (actually, the n+1st), we use the original measure, m . Convince yourselves that (S, Á S, l ) is an atomless measure space. Consider the extreme sets. For the original blocking coalition S, note that the first component is non-positive, ò S [y(h) - e(h)] £ 0 and the second strictly positive, m (S) > 0. Consider Æ Î Á , then l (Æ ) = (0, 0). Thus, by Lyapunov's theorem on vector-valued measures in atomless measure spaces, a l (S) + (1-a )l (Æ ) = a l (S) Î {l (B) | B Î Á S} for any a Î [0, 1]. Now, consider r = e /2m (S). As m (S) > 0 and m (S) > e (otherwise we are done), then 0 < r < 1. Thus let a = r , so that we know r l (S) Î {l (B) | B Î Á S}. But note that:
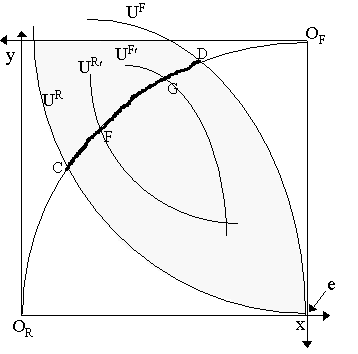
Now, by Lyapunov's theorem, there must be a set E Î Á S such that l (E) = r l (S). Thus, we know that l (E) = [ò E [y(h) - e(h)] dm , e /2]. As r > 0, then ò E [y(h) - e(h)] dm = r (ò S [y(h) - e(h)] dm ) £ 0 and m (E) = e /2 < e . Thus, we have found a sub-coalition (E) which is feasible and has a positive measure which is smaller than e . To wind this up, we need to check that E Î Á S is also a member of Á . Well, recall that E was constructed by taking intersection of S and some other set A Î Á , i.e. E = S Ç A.. But countable intersections are in the original s -algebra, i.e. if A, S Î Á , then S Ç A = E Î Á .§ To recap, Schmeidler's theorem says that if we have a coalition S which blocks an allocation x with allocation y, then we can find an arbitrarily small (but of positive measure) sub-coalition E that can also block allocation x with y. Thus, in an atomless economy, C(E) = Ce (E) for any e . Schmeidler's theorem is surprising for it says, in a continuum economy, that the work that is done by huge coalitions can be also be done by very small coalitions. Schmeidler's original results were strengthened by Karl Vind (1972). Specifically, he demonstrated that if there is a coalition S which can block allocation x with allocation y, then not only is there (as Schmeidler shows) a smaller coalition which blocks that allocation, but we can find a smaller coalition of any size to block it, i.e. for any d where d £ m (S), we can find a coalition T of size m (T) = d that can block allocation x with allocation y. Birgit Grodal (1972) took it one step further and imposed a different type of restriction: she asked what would happen if we not only restricted the size, but also the composition of the coalition. In other words, what if we restrict coalitions to a radius of "neighboring" agents, i.e. people with similar preferences and endowments. She shows that we obtain the same result for a continuum economy: any allocation x that can be blocked by a coalition S can be also be blocked by a smaller coalition of less diverse people. One suspects -- as one always should in such cases -- that Schmeidler's result only makes sense in the extreme limiting case of a continuum economy. The continuum, after all, has a habit of stuffing rabbits into the hat that we cannot find in the finite case. But M. Ali Khan (1974) demonstrated that Schmeidler's result is more general. Given a non-standard formulation, Khan showed that in a "large but finite" economy, that if we place restrictions on coalition-formation, the core is enlarged (of course), but it is "not much" larger -- with the terms in quotations given a rather precise meaning. The implication of these results seem to be that the more agents there are in the economy, the smaller the relevance of placing restrictions on coalition formation. Why this is so ought to be somewhat intuitive. Consider the replication economy: let us say we have two Robinsons and Fridays. Now, as we know, this will reduce the size of the core. In Figure 2, the core with two Robinsons and two Fridays is represented by the contract curve segment between F and G. This is because allocations such as C and D can now be blocked by three traders (e.g. two Robinsons and a Friday can block C).
Now, in a four-person economy, if we impose the restriction that the maximum m (S) = e = 1/2, then only coalitions of two people or less are possible. Thus, allocations C and D will no longer be blockable. But note that allocations off the contract curve and within the lens formed by UR and UF will still be blockable (it is enough for a Friday and a Robinson to get together to block such allocations) . Thus, in a four-person economy, the restriction e = 1/2 enlarges the core from the FG segment of the contract curve to the CD segment of the contract curve. Only if we impose e = 1/4, will the entire lens area between UR and UF form the e -core -- and we have to impose e < 1/4 to obtain the whole box as e -core. Notice that a restriction e = 3/4 (or higher) will not affect things. Comparing this with our previous case, we see that restrictions matter more in the two-person economy than they do in the four-person economy, e.g. the restriction e = 3/4 doesn't affect the four-person core; but it will enlarge the two-person core to the entire lens. So what Schmeidler is telling us is that in the limiting case of an infinite number of people, restrictions don't matter at all. If the core is equal to the e -core, then by extension (via Aumann's theorem), the e -core is equivalent to the set of Walrasian equilibrium allocations. Andreu Mas-Colell (1982) has attempted to give some interpretative economic teeth to this result. Specifically, he argued that we need not tether ourselves to the credulity-stretching informational requirements of the "idealized" notion of free Edgeworthian recontract. If whatever can be done by a coalition, can be done by an arbitrarily small coalition, then one only needs a "few" well-informed people to take us to Walrasian equilibrium. Mas-Colell suggests that we think of these few as the "arbitrageurs". With the rest of the people in the economy remaining passive, it is enough for this small, profit-seeking group to do their duty -- and take us to equilibrium.
|
All rights reserved, Gonšalo L. Fonseca