Complex Conjugate Pairs

Back

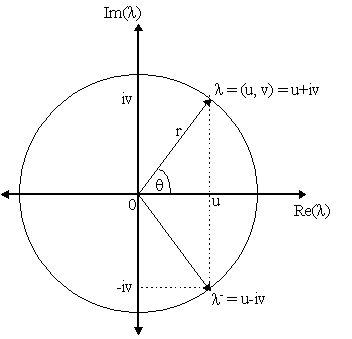
It might be worthwhile stating a few facts about complex numbers. Let l = (u, v) be a complex number, where u is the real part of l (denoted Re(l ) = u) and v is the imaginary part (denoted Im(l ) = v). The complex number l = (u, v) can be written as l = u + iv where i is the imaginary operator, i = Ö -1.

If l = u + iv is a complex number, then the l^- = u - iv is called the "complex conjugate" of l . Note that if Im(l ) = 0, then l = u = l ^-, i.e. the complex conjugate of any real number is that real number. Note also that the sum of a complex number with its complex conjugate is a real number, i.e. l + l ^- = (u + iv) + (u - iv) = 2u and the product of a complex number with its complex conjugate is a non-negative real number, i.e. l l ^- = (u+iv)(u-iv) = u² + v² (as i² = 1).

The "absolute value" or "modulus" of a complex number l = u + iv is the non-negative real number |l | defined by |l | = Ö (u² + v²). Note that the definition of absolute value for a real number is no different as |u| = Ö (u²) when the complex number is itself a real number. We can represent complex numbers and their conjugates as ordered pairs in the plane defined by a real and an imaginary axis as shown in Figure 1.

Introducing polar coordinates r, q by setting u/r = cos q and v/r = sin q where r = |l |, then the complex number l = u+iv can be written as l = r(cos q + i sin q ). A complex number l expressed in this form is said to be in "polar form".

We want now to define the exponential function, ¦ (l ) = e^l where l is a complex number such that the laws of exponents hold, i.e. e^xe^y = e^x+y and e⁰ = 1. If l = u + iv, then we want e^u+iv = e^ue^iv, so we have to define e^iv. This can be done as follows: let e^iv = cos v + i sin v. Thus, for l = u + iv we obtain e^l = e^u(cos v + i sin v). Thus, if l is real so that v = 0, then e^l  = e^u(cos 0 + i sin 0) thus, as cos 0 = 1 and sin 0 = 0, then e^l  = e^u. Similarly we can note that if we have two complex numbers, l = u + iv and l ¢ = u¢ + iv¢ , then e^le^l¢ = e^ue^u¢ (cos v - i sin v)(cos v¢ + i sin v¢ ) = e^ue^u¢ [(cos v cos v¢ - sin v sin v¢ ) + i(cos v sin v¢ + sin v cos v¢ )] = e^u+u¢ [(cos (v + v¢ ) + i(sin (v + v¢ ))] = e^{l+l ¢} by the properties of cosine and sine. Similarly, we can note that e^l = e^-l = e⁰ = 1. Thus, the laws of exponents hold.

Finally, as l = u + iv can be expressed in polar form l = r(cos q + i sin q ) but, recall, e^iq = cos q + i sin q , then l can also be expressed as l = re^iq where r = |l |. Thus the complex number l can be expressed in the following four forms:

l = (u, v) = u + iv = r(cos q + i sin q ) = re^iq

so, given u and v, we can determine r and, confining attention to [0, 2p ), also q . Similarly, knowing q and r, we can find u and v. Finally, De Moivre's theorem can be obtained by noting that l ⁿ = (re^iq )ⁿ = rⁿe^inq = rⁿ(cos nq + i sin nq ).

Back

Top

Selected References

Next