|
Contents (A) Compactness and Continuity: Preliminaries (A) Compactness and Continuity: Preliminaries Let (X, r ) be a metric space, with X as the space and r as the associated metric. Then, in any given metric space (X, r ), the following things may be defined:
(Closed/Open Complementarity) E is open iff Ec closed. Proof: (i) Suppose Ec closed. Consider any x Î E. As Ec closed, then x Ï Ec and x not limit of Ec. Thus, it must be that there is an e such that Ne(x) Ç Ec = Æ . This is true for all x Î E. Thus, E open. (ii) Suppose E open. Consider x = lim Ec. Then, Ne(x) Ç Ec ¹ Æ for all e > 0. Thus, x is not an interior point of E. Since E is open and x is not an interior point of E, then it must be that x Î Ec. Thus, Ec is closed.§
Proof: (i) Let ¦ be continuous function. Choose x0 Î X. Then consider an open subset G Ì Y where ¦ (x0) Î G. As G is open, then ¦ (x0) is in the interior of G so that we can then define Ne[¦ (x0)] Ì G, i.e. an open e -ball around ¦ (x0). By continuity of ¦ at x0, we know that there is a d > 0 such that ¦ (Nd(x0)) Ì Ne[¦ (x0)] Ì G, thus Nd(x0) Ì ¦ -1(G). As Nd (x0) is an open d -ball within ¦ -1(G), then x0 is an interior point. Thus ¦ -1(G) is open.Ne (ii) Suppose ¦ -1(G) is open for every open set G Ì Y. As G is open, we can define an open neighborhood Ne [¦ (x0)] Ì G for any ¦ (x0) Î G. As ¦ -1(G) is open in X, then ¦ -1(Ne[¦ (x0)]) is open ball in X which contains x0. Thus, there is a neighborhood Nd(x0) Ì ¦ -1(Nd [¦ (x0)]). Thus, ¦ (Nd(x0)) Ì Ne (¦ (x0)). Thus ¦ is continuous in X.§
Thus, we approach one of the more important important theorems regarding a special type of metric space - the Euclidian space Rn:
Proof: We want to prove (a) Þ (b) Þ (c) Þ (a). For this we need the following two lemmas:
Proof: In = [an, bn], thus we have a collapsing sequence of intervals. Let E = {a1, a2, ... } be the set of lower bounds. Obviously, E is non-empty and bounded above by b1 (the upper bound of the largest interval). Let x = sup E, i.e. the sup of the lower bounds. If m and n are positive integers, then an £ am+n < bm+n < bm, thus x < bm for each m Î 1 2, .... But, as x = sup E, then x ³ am. Thus, x Î [am, bm) for each m = 1, 2, .... or, simply, x Î Im for m = 1, 2, ... or x Πǥn=1In ¹ Æ . Q.E.D.
Proof: If B is a box, then B = {x Î Rn ½ ai £ xi £ bi for i = 1, ..., n}. Thus, box Bk = {x Î Rn ½ aki £ x £ bki for i = 1, .., n.} and {Bk} is a sequence of collapsing boxes. Let interval Bki = [aki, bki]. Consider sequence {Bki} where Bki É B(k+1)i ...., i.e. a sequence of collapsing closed intervals. By previous lemma, Ç¥k=1 Bki ¹ Æ , i.e. there is a xi such that xi Î Bki for all k = 1, ..., n. Of course, this is true for all i, thus x = [x1, ...,xi, ... xn] Î Bk for all k = 1, .., n, i.e. x Πǥk=1 Bk. Q.E.D (a) Þ (b) (Heine-Borel Theorem): If E is bounded, we can enclose E in box B, i.e. E Ì B = {x Î Rn ½ ai £ xi £ bi, i = 1, .., n}. If B is compact, then as E is a closed subset of a compact set, is also compact. Thus, we claim B is compact. Proof: If not, then {Ga } is an open cover for B, but there is no finite sub-cover. Now, consider the following: for every i, Bi = {x Î R½ ai £ xi £ bi}. Define d = Ö [å ni=1 (bi - ai)] so, for all x, y Î B, r (x, y) £ d . Now, consider ci = (ai + bi)/2, i.e. ci bisects every interval Bi into two intervals, [ai, ci] and [ci, bi]. Thus, {ci} divides B into 2n boxes, call then Qj Ì Rn where È jQj = B. Now, recall that {Ga }is an open cover for B, thus there must be at least one Qj that is not covered by any finite subcollection of {Ga} (otherwise B is compact). Call Qj = B1. Thus, r (x, y) £ d /2 for any x, y Î B1. Subdivide B1 again by bisection, e.g. there is a di = (ai + ci)/2, etc. Thus, we subdivide B1 into 2n boxes Jj whose union È jJj = B1. So, define B2 as the "uncovered set" where B2 Ì B1. Obviously, r (x, y) £ d /4 for any x, y Î B2. Continuing the process of subdividing eternally, then we obtain a sequence of boxes B É B1 É B2 .... where any Bk in this sequence is not covered by any finite subcollection of {Ga}. Obviously, for any x, y Î Bk, r (x, y) £ d /2k. However, by previous lemma, there is an x Î Rn such that x Î Bk for all k = 1, 2, ...., i.e. $ x Πǥk=1 Bk. But x Î B and {Ga } is an open cover of B, thus there is some a such that x Î Ga . At this point, define Ne (x) = {y Î Rn ½ r (x, y) < e } as an open e -neighborhood of x. But, as Ga is open, then for any e > 0, there is a y such that y Î Ne (x). But as {Bk} is an eternal subdivision, we can fit a box inside of Ne (x), i.e. there is some Bk (k sufficiently large) such that Bk Ì Ne (x), which implies that r (x, y) > d /2k. But then, when this box is fitted, we need divide no further. Thus, for any Bk, there is some Ga such that Bk Ì Ga . Thus we have a finite subcollection of {Ga } that covers B. Thus B is compact. As E is a closed subset of B, then E is compact. Q.E.D. (b) Þ (c): Suppose E Ì Rn is compact. Consider M Ì E where M is an infinite subset of E. If M has no limit in E, then for each x Î E, we would have Ne (x) with at most a finite number of elements in M. However, as M is infinite, thus no finite collection of open neighborhoods{Ne (x)} can cover it. Thus M is not compact. However, without limit points, M is closed. As M Ì E is a closed subset but not compact, then E cannot be compact. A contradiction. Thus M must have a limit point in E. Q.E.D. (c) Þ (a): we use "not (a)" Þ "not (c)" to prove this. Take two cases. Case 1: suppose E is not bounded. Then, there is points xk Î E such that r (0, xk) > k for all k = 1, 2, .... The set S of such points xk is infinite and has no limit in Rn. Thus, (c) is not true. Case 2: suppose E is not closed. Then consider point x0 Î Rn such that x0 Ï E but is nonetheless a limit point of E. Thus, there is a sequence {xn} ® x0 as n ® ¥ and xn Î E. Thus, {xn} is an infinite subset of E without limit point in E. Thus, (c) not true. Q.E.D. Thus equivalence (a) Þ (b) Þ (c) Þ (a) is proved.§ The usefulness of this theorem can hardly be overstated - but the simplest, in our case, is that in Euclidian space, if a set X is closed and bounded, then we can claim it is compact. Finally, consider the following theorem:
Proof: Let {Ga } be an open cover of ¦ (X). As ¦ is continuous, then ¦ -1(Ga) is an open subset of X for all a . Thus, Èa{¦-1(Ga )} is an open cover of X. But X is compact. Thus, there is a finite subcover, i.e. indices a 1, ..., a n such that X Ì È a in{¦ -1(Ga i)}. Since, by continuity, ¦ (¦ -1(E) Ì E for all E Ì Y, then ¦ (X) Ì È a in ¦ {¦ -1(Ga i)} or ¦ (X) Ì È a in{Ga i}. Thus, we have a finite subcover of ¦ (X). Thus, ¦ (X) is compact.§ (B) The Weierstrass Maximum Theorem We want to prove the Weierstrass Theorem, i.e. that a continuous, real-valued function over a compact set attains a maximum and a minimum. For this we need the following lemma:
Proof: If s Î E, then s Î cl(E). Suppose s Ï E, then for every e > 0, there is a z Î E such that s - e < z < s, otherwise s - e would be an upper bound for E. But, then, for all e > 0, there is a z Î Ne (s), thus s is a limit point of E. Thus, s Î cl(E). We can do the same for t = inf E.§ Now we can turn to the Weierstrass Maximum Theorem (Th. 1.7.4’ in Debreu, 1959): (Weierstrass) let ¦ : X ® R be a continuous real-valued function on a non-empty compact metric space X. Let M = supxÎ X ¦ (x) and m = infxÎ X ¦ (x). Then, there is a point xM and a point xm in X such that ¦ (xM) = M and ¦ (xm) = m, i.e. a continuous function ¦ (·) attains a maximum and a minimum over a compact metric space. Proof: X is compact. Thus, by the earlier theorem, ¦(X) is compact. By Heine-Borel, ¦ (X) is closed and bounded. As ¦ (X) is a closed and bounded set of real numbers, then ¦ (X) = cl¦ (X) and thus, by the previous lemma, contains its own supremum and infimum, i.e. sup ¦ (X) Î ¦ (X) and inf ¦ (X) Î ¦ (X).§ (C) Upper and Lower Semicontinuity of Correspondences What can we say about cases when we are not dealing with single-valued functions but rather correspondences (i.e. set-valued functions)? Thus, a correspondence j : X ® Y maps to a set and not a point, e.g. X Í Rm and Y Í Rn. How do we define the "continuity" for a correspondence? A different approach must be followed.
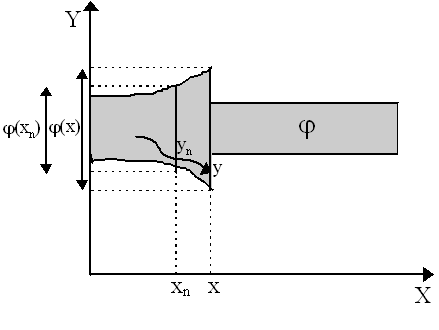
Intuitively, we can see this criteria graphically in Figure 1: given a sequence {yn} in the graph of the correspondence which approaches some endpoint y, does this endpoint y lie in the graph of j (x)? If so, then the correspondence is "upper semicontinuous". We can see this in the figure below where any sequence {yn} drawn in the graph of the correspondence will approximate a point (e.g. y) within the graph of the correspondence.
We now turn to an interesting theorem:
Proof: As this is an "if and only if" statement, we need to prove it both ways. (i) usc Þ closed graph: Let j be upper semicontinuous. Then for all yn in the convergent sequence yn ® y, it is true that yn Î j (xn) " xn ® x. Thus, by the definition of the graph of j , it is true that (xn, yn) Î Gj " xn, yn in their respective convergent sequences. As (xn, yn) converges to (x, y), by the definition of u.s.c., then (x, y) is a limit point of the graph of j . Is (x, y) Î Gj ? Again, yes, as by the definition of u.s.c., y Î j (x). Thus every convergent sequence (xn, yn) in Gj has its limit in Gj . Thus Gj is closed. (ii) closed graph Þ usc: If Gj is closed, then every convergent sequence (xn, yn) Î Gj has its limit (x, y) in Gj . This implies that for all sequences xn ® x, yn Î j (xn), yn ® y, then y Î j (x), i.e. it cannot be that the first three properties are fulfilled and the last (y Î j (x)) is not for that would mean that (x, y) Ï Gj and thus Gj would not be closed. Thus j is upper semicontinuous at x. Since x is arbitrary, then this is true for any x Î X. Thus, j is upper semicontinuous.§ Note: the assumption in this proof that the range of the correspondence j is compact can be seen to be necessary. A counterexample can be constructed of a closed graph which is not u.s.c. if the range fails to be compact. Consider the following correspondence: j (x) = {1/x} for x > 0 and j (x) = {0} for x = 0. There is indeed a closed graph, but it is not u.s.c. at x = 0. Also, for the first part of the proof, that we must assume that the domain X is closed - or else j (.) may not be defined at x. The sum and Cartesian product of a series upper semicontinuous correspondences is also upper semicontinuous.
Proof: Let us have convergent sequence{xn} in X where xn ® x and consider a sequence {yn} in Y where yn Î j (xn) and where j (xn) = å ki=1j (xn) and yn = å ki=1yni with yin Î j i(xn). As j i is upper semicontinuous, then there is a yi Î j i(x) such that the sequence {yni} converges to it, i.e. yni ® yi. As this is true for all i = 1, .., k, then limn® ¥ å i=1k yni = å i=1k yi and å i=1k yi Î å i=1k j i(x) = j (x). Defining y = å i=1k yi, then limn® ¥ yn = y and y Î j (x). Thus j is upper semicontinuous.§ The next theorem is practically the same:
Proof: Let us have convergent sequence{xn} in X where xn ® x and consider a sequence {yn} in Y where yn Î j (xn) and with j (xn) = Õ ki=1j (xn) and yn = [yn1, yn2, .., ynk] with yin Î j i(xn). As j i is upper semicontinuous, then there is a yi Î j i(x) such that the sequence {yni} converges to it, i.e. yni ® yi. As this is true for all i = 1, .., k, then limn® ¥ [yn1, yn2, ..., ynk] = [y1, y2, ..., yk] and [y1, y2, .., yk] Î j 1(x)´ j 2(x)´ ..´ j k(x) = Õ i=1k j i(x). Defining y = [y1, y2, .., yk] and recalling that Õ i=1k j i(x) = j (x), then limn® ¥ yn = y and y Î j (x). Thus j is upper semicontinuous.§ Let us now turn to the analogous concept of lower semicontinuity:
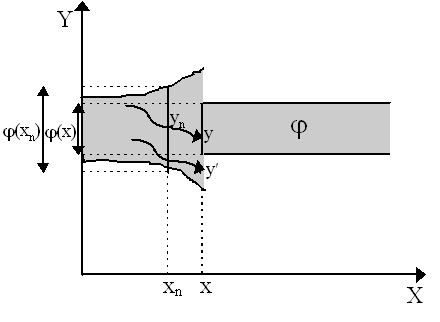
Intuitively, we can see this criteria graphically again, this time in Figure 2: given an endpoint y Î j (x) in the graph, is there a sequence {yn} in the graph that approaches it? If so, then the correspondence is "lower semicontinuous". In the earlier Figure 1, we do not have a lower semicontinuous function at x as the point y Î j (x) cannot be approximated from the right by a sequence of points in the graph. However, in Figure 2, the correspondence is indeed lower semicontinuous as any endpoint y in j (x) is approximated from either side by a sequence {yn} in the graph. However, the graph below is not upper semicontinuous as, for instance, we can imagine a sequence in the graph approximating y¢ yet y¢ Ï j (x).
Finally, we should note that the sum and product of a series of a lower upper semicontinuous correspondences is also lower semicontinuous, i.e. correspondence j : X ® Y where j = å i=1kj i or j = Õ i=1kj i are lower semicontinuous if the series {j i}i=1k where j i:X ® Y is also lower semicontinuous. The proof is analogous to that of the upper semicontinuous case. Finally we turn to continuity:
Thus, in the previous figures, the correspondences are not continuous as the first is upper semicontinuous (but not lower semi-continuous) while the second is lower semicontinuous (but not upper semi-continuous). The following theorem (Berge's Theorem, i.e. Th. 1.8.4 in Debreu, 1959) is very useful. Let ¦ : Rn ´ Rm ® R and j : Rm ® Rn (i.e. ¦ is a function and j a correspondence). Then let:
thus, f(t) is a function and F(t) is a correspondence (for "argmax" read "the argument (x) that maximizes ¦ (x, t)"). Then the following holds:
Proof: Omitted. See Hildenbrand (1974: p.30) or Border (1985: p.64) Kim C. Border (1985) Fixed Point Theorems with Applications to Economics and Game Theory. Cambridge, UK: Cambridge University Press. Gerard Debreu (1959) Theory of Value: An axiomatic analysis of economic equilibrium. New York: Wiley. Werner Hildenbrand (1974) Core and Equilibria of a Large Economy. Princeton: Princeton University Press. Hukukane Nikaido (1968) Convex Structures and Economic Theory. New York: Academic Press.
|
All rights reserved, Gonçalo L. Fonseca