|
Robert J. Aumann's (1964) core equivalence theorem states that the set of core allocations in his atomless economy is identical to the set of Walrasian equilibrium allocations, i.e. C(E) = W(E). The method of proof we follow here is not identical to Aumann's original. In particular, we make use of some rather simplifying procedures -- notably, we use Aumann's (1965) definition of "integration of correspondences" and Lyapunov's theorem (introduced into economics by Karl Vind (1964)). However, the essence of the proof is basically the same. Aumann's (1965) definition of the "integral of a correspondence" was actually one of the few recorded cases where an economist has actually contributed to the mathematical theory. The problem Aumann faced was effectively this: we know how to integrate a function ¦ : X ® R, where ¦ (x) is a single point in R, but there was no standard means to integrate a correspondence, j : X ® R where j (x) is a set in R rather than a single point. Aumann (1965) provided the following definition:
In other words, facing a correspondence, j : H ® R, take a measurable function that passes everywhere through j . Integrate it (if you can -- but you usually can integrate measurable functions). Put it in a bag. Find another measurable function, integrate it, put in the same bag, etc. Do this again and again for all measurable selections from j . Put them all in the bag. Then the "integral of correspondence j " is merely this bag, a set of integrals of measurable selections from j . That's it. Now, this may not look useful: we just have a set full of numbers (the integrals of the measurable selections, ¦ ). However, there is a very interesting property of Aumann's integral: namely, it is a convex set. Hello? A convex set? This should sound surprising. Let g and ¦ be measurable selections of j . Then, ò H ¦ and ò H g are numbers, both of them included in the "bag" ò H j . But to say the ò j is a convex set means that a (ò H ¦ ) + (1-a )(ò Hg) Î ò H j for a Î (0, 1), i.e. the convex combination between these two numbers, ò H ¦ and ò H g, is also in the set! This means there must be some measurable selection of j (call it k) where a (ò H ¦ ) + (1-a )(ò Hg) = ò H k. This is not intuitive. How can this be true? But it is true. And we'll find, time and time again, that things like this are true. This is because infinite numbers of things have a tendency to"convexify" collections of things that, individually, are not convex. It is is easy to visualize this. In simple R2 space, take, say, a circle with a slight dent in it, so that it is nearly convex, but not actually so. Take another circle with a slight dent elsewhere in it. Add them together, and you'll get a circle with two dents -- but the "dents" are relatively "smaller" in this big circle than they were in the original. Add up a lot of circles with lots of different dents, and you'll see that, slowly, the dents begin to disappear. In the limiting case of an infinite number of circles, the resulting "sum" will be a completely convex circle. It is effectively this kind of "convexifying" property of infinite numbers that yields the "convexity" of the integral of a correspondence, ò H j , even though it might not seem obvious. To prove this we need to use Lyapunov's theorem, introduced by Vind (1964). We merely state the theorem:
Proof: Omitted. See Vind (1964: Lemma A). Now we come to the main result:
Proof: From Debreu (1967: p.369-70) (originally attributed to H. Richter). Let x, y Î òH j . By Aumann’s definition, there are measurable selections ¦ and g such that x = òH ¦ dm and y = òH g dm , where m is an atomless measure. It is an easy matter to recall that if ¦ and g are integrable, then the integrals ò H ¦ and ò H g also serve as measures, i.e. given S Î Á , then we can measure it with ò S ¦ or ò S g. Thus, let us define the vector l (S) = (ò S ¦ , ò S g). We skip the part proving l is atomless, so take this on faith. Now, by Lyapunov’s Theorem, the set {l (S) = (òS ¦ , òS g) Î R2 ½ S Î Á } is convex. Now, as Æ , H Î Á , then l (Æ ) = (0, 0) and l (H) = (x, y). Since both (0, 0) and (x, y) belong to this set, so does their convex combination a(x, y) + (1-a)(0, 0) = (ax, ay), for any a Î [0, 1]. Thus, there must be a set E Î Á such that l (E) = (a x, a y), i.e. there is an E where ax = òE ¦ dm and a y = òE g dm . Define function k(h) = ¦ (h) if h Î E and k(h) = g(h) if h Ï E. Then:
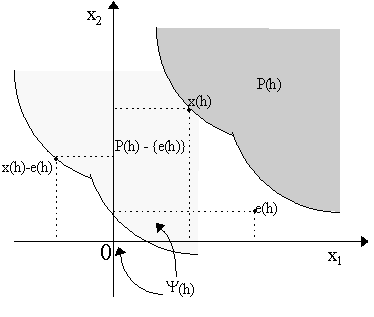
Now, as k is composed of measurable selection ¦ over E and of another measurable selection g over H\E, then k is itself a measurable selection of j , and so ò H k Î ò H j . However, as we have just shown, ò H k = a x + (1-a )y, thus a x + (1-a )y Î ò H j . So ò H j is convex.§ Why do we need this anyway? Well, we shall be integrating correspondences very soon. In particular, we shall consider a rather important correspondence -- the strict upper contour set of preferences. For an individual, the strict preference set, which we shall label simply P(h), is the set of allocations individual h strictly prefers to his current allocation, x(h), i.e.
Thus, P(h) is the set of points in Rn above the indifference curve of agent h that passes through x(h). As we have not assumed convexity of preferences in this model, then P(h) is not necessarily a convex set. (see Figure 1 below). Varying the household name, h, we vary the consequent upper contour set, P(h). Thus, we can define a correspondence:
which maps household names to subsets of Rn. We will be using this in the core equivalence theorem that follows. [To remind, see our page for notation and definition of an atomless economy, W(E) is the set of Walrasian equilibria and C(E) is the Edgeworthian core.]
Proof: Originally Aumann (1964). We effectively take the version in Hildenbrand (1974: p.133-5). [For an alternative proof which does not use the integral of a correspondence, see Hildenbrand (1982: p.843-5).] As this is an equivalence theorem, we must prove that W(E) Ì C(E) and that C(E) Ì W(E). The first we are already familiar with: (i) W(E) Ì C(E): Suppose not. Then, $ x Î W(E) such that x Ï C(E). Then there is some coalition S Ì H and a bundle y such that y(h) >h x(h) for all h Î S and ò H y £ ò H x. But, if so, then multiplying by p ¹ 0, it will be true that: ò H py £ ò H px. But then this violates the definition of a Walrasian equilibrium as we have found a bundle y and at least one agent h such that y(h) >h x(h) does not imply ò H py > ò H px. Therefore, x Ï W(E). A contradiction. (ii) C(E) Ì W(E): We shall undertake the rest of the proof of Aumann in several steps. Firstly, let us define the correspondence Y(h) = {P(h) - {e(h)}}È {0}, i.e.
So, Y (h) is the net trade version of the strict upper contour set for preferences of agent h seen from his equilibrium allocation, x(h), plus the (no trade) origin. See Figure 1 for intuition. Thus, integrating this:
for which we are using the Aumann definition of an integral of a correspondence. By the assumption that (H, Á , m ) is atomless, then L is convex by the previous Lemma (Lyapunov's Theorem, etc.). Furthermore, as 0 Î L, it is non-empty.
This L is analogous to the one we used in Debreu-Scarf (1963). In fact, the subsequent method of proof follows the same logical steps. Our first step is to prove that L Ç Rn- = {0}, i.e. L does not intersect the interior of the negative quadrant. To prove this, suppose not. Suppose there exists a z Î L, where z << 0. Then by the Aumann definition of the integral L, there is a measurable selection y in Y such that z = òH y(h) << 0. Consider then a set of agents S = {h Î H ½ y(h) ¹ 0} where m (S) > 0. This will serve as our coalition. As z = òH y(h) = ò H\S y(h) + ò S y(h), then as y(h) = 0 for all h Ï S, then òH y(h) = ò S y(h) << 0. But now as z Î L, then we can construct a bundle (y + e) such that y(h) + e(h) >h x(h) for all h Î S. Then integrating over S, we get ò S [y(h) + e(h)], which is the average allocation received in the coalition. However, as ò S y(h) << 0, then:
which is another way of saying that the allocation (y + e) is feasible for the coalition S. But as we constructed it, (y(h) + e(h)) is also preferred to x(h) by the members of the coalition h Î S. And, by construction, m (S) > 0. So x(h) cannot be in the core. A contradiction. So far so good. Now, in the second step, we want to use the separating hyperplane theorem as we did in the Debreu-Scarf case and separate L from the interior of the negative orthant. Now, as L Ç Rn- = {0}, then L Ç -Rn++ = Æ. We also know that L is non-empty (as 0 Î L) and, by Lyapunov's theorem, convex. As a result we can employ the separating hyperplane theorem to separate L from the strictly negative orthant, i.e. by the SHT, there is a vector p and a scalar c such that py ³ c " y Î L and py £ c for every y Î -{Rn++}. But by construction, 0 Î L, thus, py ³ 0 " y Î L. Now, if y Î L then y = òH Y(h). Following Hildenbrand (1974: p.63, Prop. 6), we can interchange infimum and integral:
but by SHT, py ³ 0 " y Î L = òH Y(h). Thus,
Since, by definition, 0 Î L, then 0 Î Y(h) a.e. in H. Consequently, inf p· Y(h) £ 0. Combining, then, we see that inf p·Y(h) = 0 almost everywhere in H. Notice that this implies that for all y Î P(h), then p·y ³ p·e(h), i.e. if y >h x(h), then p·y ³ e(h) almost everywhere in H. Thus, we have a quasi-equilibrium. As we know, by ò H e(h) >> 0 and strong monotonicity of preferences, it is a simple matter to transform this result into a Walrasian equilibrium, i.e. almost everywhere in H, y >h x(h) implies p·y > p·e(h). § In sum, Aumann's theorem has proved that C(E) = W(E), that in the atomless economy, the set of core allocations is the set of Walrasian equilibrium allocations. Through these elaborate mathematical means, Edgeworth's conjecture (b) is proved.
|
All rights reserved, Gonçalo L. Fonseca