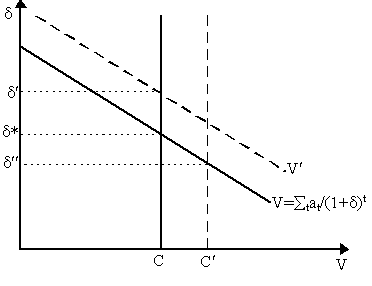
More elaborate considerations of Keynes's theory, however, were forced to ask what is the internal rate of return? This is far from evident. Keynes defined the internal rate of return as the "marginal efficiency of capital", which Abba Lerner (1944, 1953), more accurately, rebaptized as the "marginal efficiency of investment" (MEI). Keynes claimed that this could be defined as follows: "I define the marginal efficiency of capital as being equal to the rate of discount which would make the present value of the series of annuities given by the returns expected from the capital asset during its life just equal its supply price" (Keynes , 1936: p. 135)In contrast, Keynes defines the "supply price of the capital asset...not the market price at which an asset of the type in question can actually be purchased in the market, but the price which would just induce a manufacturer newly to produce an additional unit of such assets, i.e. what is sometimes called its replacement cost" (1936: p.135). Consequently: "The relation between the prospective yield of a capital asset and its supply price or replacement cost, i.e. the relation between the prospective yield of one more unit of that type of capital and the cost of producing that unit, furnishes us with the marginal efficiency of capital of that type" (Keynes , 1936: p.135).In order to come to grips to what Keynes is talking about, we need to disentagle his English a bit. Let a1, a2, a3, .., etc. be the expected stream of returns of a particular investment project. Consequently, at a given rate of interest r, the market present value of these returns is merely åt at/(1+r)t where we are summing from t to infinity. Let C be the cost of undertaking the project - or rather, the replacement cost of capital or "supply price" of capital goods (i.e. what the capital goods industries sell them for). Then, Keynes proposed that the internal rate of return (or marginal efficiency of investment) would be the discount rate d * where: åt at/(1+d *)t = CWe can conceive of this via Figure 3 in return/present value space. Consider the line V which denotes the present value of a particular project at different discount rates d . Obviously, as the discount rate d increases, then the present value of that particular project declines, i.e. V = å tat/(1+d )t falls as d rises. The replacement cost of capital, C, is given exogenously by the capital goods industries. Thus, the marginal efficiency of investment MEI, or "internal rate of return", of this particular project is defined here as d *, i.e. the d that equates the present value of the project with its capital cost. Whether this particular project will be undertaken or not, then, depends on the rate of interest on the bond market - specifically, if d * > r, then this project is undertaken; if d * < r, then it is shelved.
Figure 3 - Keynes's Internal Rate of ReturnSeveral things can already be noted from Figure 3. The first is that if expectations or "animal spirits" are bouyant enough such that the expected stream of returns on this project rises (i.e. {at} rise) then the V curve will shift to the right (e.g. to V¢ in Figure 3) and, consequently, the corresponding internal rate of return will increase (to d ¢ in Figure 3). Conversely, if the supply price of capital rises (C rises to C¢ for instance), then the corresponding internal rate of return on this project declines (to d ¢ ¢ in Figure 3). However, all this is for a single project. The rest of the story must be told and, for this, we must consider an array of investment projects. For each project in this array, we can compute the internal rate of return d * on the basis of the projected stream of retrurns ({at}) of that project and its supply price (C). Suppose we then rank the investment projects according to their internal rate of return d *. Then, we could obtain a MEI schedule which descends from the project with the highest d * to that with the lowest d *. This is shown heuristically in Figure 4 where we have six "lumpy" investment projects: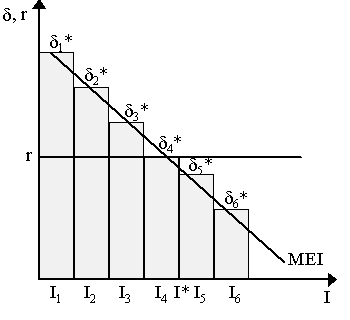 
Figure 4 - Marginal Efficiency of Investment (MEI) ScheduleThe histogram in Figure 4 represents the six projects (I1, I2, .., I6) with six internal rates of return (d 1*, d 2*, .., d 6*) ranked accordingly from highest to lowest. Thus, at a given interest rate r, only projects I1 through I4 are "profitable", i.e. have internal rates of return greater than or equal to r, while projects I5 and I6 have internal rates of return below that. Thus, the "investment" expenditure in this economy is I* = I1 + I2 + I3 + I4. If the rate of interest were lowered, it would be possible that I5 could become profitable and thus I* would increase; in contrast, if r increased, then I4 would no longer be profitable and thus I* would decrease. The MEI curve drawn in Figure 4, then, represents the equivalent of the histogram when we have many, indeed a continuum, of available investment projects. In this case, total investment will be where the rate of interest is equal to the marginal efficiency of investment curve. As a result, Keynes 's (1936) theory of investment can be expressed by the naive function I = I0 + I(r) where investment falls as the bond rate rises and rises when the bond rate falls. Bouyant expectations or animal spirits expecatations imply that all projects get valued upwards and, of course, the MEI curve shifts to the right so that the resulting I* rises. Several problems immediately emerge in Keynes's theory. First of all, as Armen Alchian (1955) and Jack Hirshleifer (1970) noted, the ranking of the projects may not be independent of the interest rates. For instance, consider two investment projects in Figure 5 whose present value curves are represented by the V1 and V2 schedules respectively and suppose, for the sake of argument, that both have the same replacement cost of capital, C. Notice that the curves intersect at point d 0 - which is not implausible by any means. Now, if cost of capital is C for both projects, then by Keynes's argument, project 1 is more profitable than project 2 since, at C, d 1* > d 2*. Alchian (1955) argued that standard theories about the maximization of the present value of the firm read the diagram in the reverse way. Specifically, standard theories would consider the "most profitable project" to be that with the highest present value at a given rate of interest. In this case, if the rate of interest, r, is above d 0 (at rA in Figure 5, for instance) then project 1 has a higher present value than project 2 (V1A > V2A). In this case, standard present value rankings comply with the Keynesian rankings. However, Alchian noted, if the rate of interest is below d 0 (e.g. at rB), then project 2 has a higher present value than project 1 (i.e. V1B < V2B) thus by the standard theory, project 2 is superior. Here is where the standard and Keynesian theories diverge. Keynesian theory argues that even if r < d 0, project 1 would still be ranked superior to project 2 as at C , d 1* > d 2*. But standard present-value maximization theory would argue that project 2 would be superior.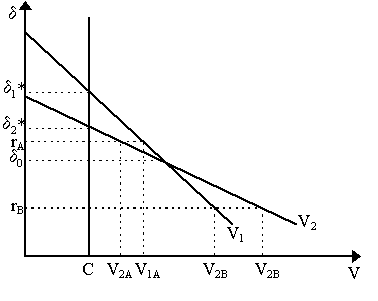 
As Alchian (1955) notes, then, Keynesian rankings are different from standard present-value maximization rankings. Or rather, Keynesian theory and standard present-value maximization are consistent only if there were only one investment project and one outside option. If there were multiple investment projects, the Keynesian ranking would be different from the present-value maximization ranking as the latter ranking is itself dependent on the rate of interest.Figure 5 - The Alchian Critique A more troublesome critique was offered up by several Post Keynesians, such as Athanasios Asimakopulos (1971, 1991) and Piero Garegnani (1978). Namely, one can question the very possibility of a downward-sloping MEI function in the presence of unemployment. In particular, we can note that Keynes's multiplier story implies that if investment is undertaken then, by the multiplier, aggregate demand and output rises. But if the marginal efficiency of investment function is dependent on expected future returns, then should not the increased income and thus aggregate demand from the multiplier imply higher future returns? If so, then the MEI function ought to shift outwards to the right. This, in turn, implies that investment ought to increase - which leads to another increase in aggregate demand and thus the MEI curve shifts out again, raising investment, etc. As a result, it is easy to conceive that, in situations of unemployment where the multiplier works its magic, investment is actually indeterminate - or rather, an ever-shifting MEI curve could imply that all investment projects will be eventually undertaken and not merely those that are profitable at the given rate of interest since the profitability of projects is itself a function of aggregate demand and thus endogenous to the problem. There are several conceivable ways of extricating Keynes's theory from this critique, none of which work exactly well. The first is simply to assert that while this ever-shifting MEI problem could be true in the aggregate, it is not true at the individual firm level. If Chrysler builds a new factory and thus pays workers more, its investment injection will not lead to an equivalent increase in demand for Chrysler cars. Rather, workers can spend their new income on Ford cars, or food or anything else, so that, at least for the Chrysler Corporation, the investment decisions it makes do not lead to one-for-one to increases in the demand for its products. However, one can also reverse this proposition: while this is true for the firm, it is still not true for the aggregate because there are no leakages to the economy. In other words, the individual firm investment function may continue to be downward sloping, but the aggregate investment function is of a different nature, i.e. horizontal. Solving this issue, then, would require a more careful consideration of the issue of aggregation. Now, Keynes himself appealed to Irving Fisher's (1930) notion - arguing that "Professor Fisher uses his "rate of return over cost" in the same sense and for precisely the same purpose as I employ the "marginal efficiency of capital"" (Keynes, 1936: p.141). However, as Garegnani (1978) points out, Fisher's bases his downward-sloping investment curve on a diminishing marginal productivity of capital argument - which can only be true if another factor (i.e. labor) is fully employed and cannot be increased. Thus, in an unemployment situation, the purported equivalence between the two concepts is not quite right. Another way of defending the falling MEI curve would be to appeal to the increasing marginal costs of investment, as suggested by Abba Lerner (1944, 1953) and later Neoclassical theorists, which may be thought of as arising from the rising supply price of new capital goods (e.g. Foley and Sidrauski, 1970). This is plausible, but one must remember that supply price of capital rises only because there are capacity constraints in the capital goods industry. That implies that either we are at full employment or we are in the very short-run and capacity cannot be increased. Garegnani's (1978) argument that Keynes's theory is supposed to be one of "long run" unemployment equilibrium, therefore would disallow the marginal adjustment cost resolution. There is one further resolution to the problem: namely, recognizing Michal Kalecki's (1937) "principle of increasing risk". Kalecki proposed that the more firms invest, the greater their indebtedness and thus the greater the potential loss if their projects fail. Thus, assessments of "profitability" become more and more conservative as firms take on larger and larger debt needed to finance greater and greater investment. This idea of "increasing risk", then, would be sufficient to yield us a downward sloping MEI curve as it neither relies on full employment nor on short run rigidities arguments. A third objection, perhaps best expressed by Robert Eisner and R.H. Strotz (1963) relates to the rather ad hoc way Keynes dealt with the determination of the expected profits and returns. They argued instead for some carefully prescribed distribution and process of expectation formation. This, of course, is a "Neoclassical" objection - Post Keynesians, such as G.L.S. Shackle (1967), Joan Robinson (1971), Hyman Minsky (1975), Paul Davidson (1972, 1993, 1994) and Asimakopulos (1971, 1991) have vociferously insisted that there is no ad hoccery there at all. Quite the contrary - pointing to Keynes's (1936, 1937) repeated insistence on radical uncertainty - indeterminate or "animal spirited" expectations are quite essential to Keynes's theory of investment. This last point is particularly noticeable as we move from Chapter 11 to Chapter 12 in Keynes's General Theory where, all of a sudden, we confront the importance of the "daily revaluations of the Stock exchange" (Keynes, 1936: p.151) on investment decisions. Although a central feature of Post Keynesian economics, this intimate relationship between financial markets (specifically stock markets) and investment/production decisions has found its way into Neo-Keynesian theory (e.g. Tobin, 1969; Blanchard, 1981) and even as far afield as in Walrasian general equilibrium theory (e.g. Diamond, 1967; Grossman and Hart, 1979). Top |
TopAll rights reserved, Gonçalo L. Fonseca