|
________________________________________________________
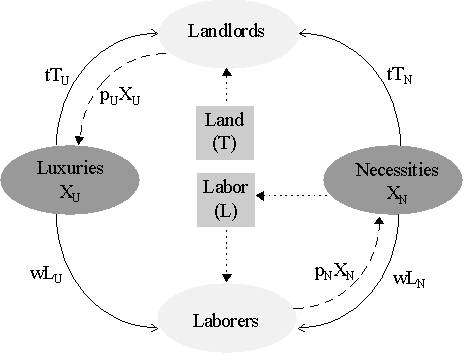
General equilibrium theory, indeed much of economics itself, owes its existence to an Irishman who lived obscurely in 18th Century France by the name of Richard Cantillon. In his remarkable Essai sur la Nature du Commerce en Generale (published only in 1755, but written c.1732-1734), Cantillon sets out, perhaps for the first time, the vision of an "economy" as a set of interacting markets connected by a price system with balanced circular flows of income between agents. Cantillon's setting was the first great breakthrough in economic theory - for it provided the fundamental structural idea behind the concept of an "economy" which was to possess all subsequent economics - Physiocratic, Classical and Neoclassical. We can set up a two-sector model of general equilibrium to illustrate the theory laid out in Cantillon's Essai. Let us have two factors (land and labor) and two goods (necessities and luxuries). Consequently there are four markets in operation and thus four prices to be discovered. To understand this, we need to step back a bit. Cantillon envisioned that we had two classes of people, landlords and laborers, the first owning land and consuming luxuries, the second owning labor and consuming necessities. As such, Cantillon foresaw there would be a "circular flow of income and expenditure" between landlords and laborers, the former contributing their land and receiving rents which they subsequently spent on luxuries, the latter contributing their labor and receiving wages and spending those on necessities. Cantillon's idea that "flows of income" were the proper subject of economic analysis was already a path-breaking insight, as it tore away from the Mercantilist obsession with the "stock of wealth". In Figure 1, we have an intuitive depiction of Cantillon's model. Income flows are represented by the solid arrows: thus income flows from the production of luxuries and necessities to the owners of land and labor. Expenditure flows are noted by the dashed arrows: landowners use their income to purchase luxuries; laborers use their income to purchase necessities. Finally, the total supply of land is assumed to be exogenous to the system, whereas the total supply of labor is endogenously determined by the amount of necessities. This is captured by the broken arrows connected to the total supply of land (T) and the total supply of labor (L).
Intuitively, it is easy to see that if flows of income, expenditure and labor supply are not "balanced" in some proper manner, then this whole economy could break down. For instance, if laborers do not receive enough wages to buy necessities, then they will starve and die, and thus goods which use labor as inputs are not produced, so that the landlords cannot buy their luxuries and they will also be deprived, etc. Whatever the form of breakdown, it is obvious that balance is hard to obtain. Yet, and this was the second crucial insight, Cantillon believed that such a balance was possible. In other words, he believed there is a way of obtaining a "natural state" or a balance of income-expenditure flows, that will not lead to a complete unravelling of the economy. The basic feature of this "natural state" is that both landlords and workers receive enough income to consume all necessities and luxuries produced ("market-clearing") and that enough of these necessities are produced to sustain a desired labor supply level. Land, which Cantillon assumes is exogenously given, is the great constraining factor: it cannot be increased. Technology, or the proportion of labor and land used in the production of the goods, is also assumed to be given. Thus, the "natural state" is conditional on the amount of land available and the production technology. If the economic system is to achieve this natural state, Cantillon reasoned, there there must be some mechanism to maintain the balance of income flows. Thus, the third great insight of Cantillon was that "natural prices" were precisely that mechanism. We must note that these natural prices are not necessarily the actual market prices in existence at any point in time. There is a difference between the "natural price" of a good - or what Cantillon called its "valeur intrisique" ("intrinsic value") - and its "exchange value" on the market at any point in time. As Cantillon writes:
Thus, "natural prices" are determined by the natural state, the balance of income-expenditure flows. In contrast, "market prices" are determined by what can be termed "demand-and-supply". Cantillon did not relate the two prices to each other very clearly: rather, as Schumpeter notes, Cantillon "was led to treat market price as a separate phenomenon and to restrict the supply and demand explanation to it. Thus emerged the...formula: normal price is determined by cost, market price is determined by supply and demand. " (Schumpeter, 1954: p.220). [As such, it is interesting to note, therefore, that not only was Cantillon the father of Classical theory, he was also, via his demand-and-supply, the father of Neoclassical theory - which is why Jevons (1881), went to such efforts to dig him out of obscurity. However, the path-breaking Cantillon was also the father of other things: via his emphasis on subjective "fancy" and his theory of entrepreneurship and uncertainty, he could be also said to be the father of Austrian economics and, via his explicit account of an endogenous flow-based quantity theory of money, he can also be said to be the father of modern monetary economics See F.A. Hayek (1936), J.J. Spengler (1954), G.L.S. Shackle (1982) and A. Murphy (1986) for retrospective accounts of Cantillon's manifold path-breaking contributions.] Let us proceed with a rather simple mathematical restatement of Cantillon's two-sector general equilibrium system (following Brems, 1986). Land (T) and labor (L) are both used to produce luxuries (XU) and necessities (XN). Nothing else is needed and the technology is a fixed proportions technology, so we can employ unit input coefficients, aTU, aTN, aLU and aLN where the coefficient aij represents the amount of input i needed to produce a single unit of output j, or aij = Fi/Xj where Fi is the factor i (in our case, either labor or land). Both labor and land are necessary to produce necessities and luxuries, so all these coefficients are positive. The amount of labor necessary to produce XN units of necessities is simply calculated as:
Thus, if we are given the size of outputs, XN and XU, then by our fixed technology, following the same logic, we can figure out the other factor demands, LU, TN, TU using the other remaining technology coefficients in an analagous way, i.e. TN = aTNXN is the amount of land employed to produce XN necessities while LU = aLUXU and TU = aTUXU are, respectively, the land and labor required to produce XU units of luxuries. Thus, the total demand for land and labor is L = LN + LU and T = TN + TU. Cantillon proposed that total land, T, was "given". But total employment, L, he thought was variable and, indeed, endogenous to the system. He noted that labor was endogenous, that is, he thought that human reproduction was "encouraged" by the consumption of necessities. This peculiar notion is a perennial, if anachronistic, concept that pervades Classical economics. As Cantillon (1755: Pt. 1, Ch.15) argued, "Men multiply like mice in a barn if they have unlimited means of subsistence," -- and went on to draw much amusing historical and anecdotal evidence for this. In sum, the amount of necessities produced, XN, will determine the total amount of labor in the economy, L. Let c be some fixed necessities-labor ratio, i.e. the amount of necessities needed to support a single laborer, c = XN/L. Thus the greater or smaller the number of necessities, then the greater or smaller the number of laborers. But what if not enough necessities are produced in the economy to sustain the given population? If there is an excess of laborers, these are, quite simply, starved off. If there is an insufficient, number of laborers, the large amount of necessities will "encourage" them to reproduce and increase. Labor supply, L, is thus endogenous to the system. Obviously, these labor supply effects probably take a few generations to work themselves out fully, thus it is clear that Cantillon is thinking in terms of a pretty long horizon of time. In this long-run, Cantillon is careful to note that there will naturally have to also be no profits. His time horizon is long enough that firms will be created and enter and exit production so as to wipe out any profit opportunities. Thus, the production processes, in the long-run, must break even: total revenues must be equal to total costs in each process. Total revenues are merely the price of the commodity multiplied by the amount produced, whereas total costs are the wages and rents paid to the labor and land employed in the production of the goods, or:
where (pN, pL) are the prices of necessities and luxuries respectively while (w, t) are the wage and rent per unit of labor and land respectively. Now, if the system is to be balanced in the long run, then enough necessities much be produced to sustain the amount of labor desired. But if this is to be so, then the total wage bill over both industries (wL) must be sufficient to buy up all the necessities at the going prices (pNXN), i.e. wL = pNXN. If not, as Cantillon noted, population will change (for more or for less) and thus we will not have a long run balance. With this condition, we can easily note that plugging this in to our first revenue-cost equality, that:
or as wL = w(LN+LU) by the definition of L, then wLU = tTN. But then plugging this into our second price-cost equality:
so, obviously, we attain a second condition: pUXU = tT, by the definition of T. Thus, the rent bill received by landlords must exactly pay for the production of luxuries. These are the conditions for a long-run, sustainable economic system. The issue is now whether we can find a set of prices (w, t, pN, pU) which can maintain such a system. The solution is straightforward. Given the labor survivability condition, c = XN/L, and knowing that wL = pNXN, then obviously:
the "real wage" is merely the cost of sustaining of a single laborer alive. What about rent? Well, let us divide our revenue-cost equalities by the respective outputs of labor and land, so:
which merely states that the price of a commodity must equal the cost of production of a single unit of it (note our use of the definition of unit input coefficients). Now, from our definition of the real wage, w = cpN, so plugging that into our first price-cost equality:
and re-arranging:
we obtain the price of the necessary good. For the luxury good, we start by doing the same:
only now we use our expression for pN and obtain:
thus, solving for t/pU, after some algebraic manipulation:
where t/pU is the "real rent" rate. Thus, we have obtained expressions for real wages and real rents as a function of the "technological" coefficients. Thus, apparently, no other consideration was necessary. The factor prices seem to be completely determinate. Or are they? We have yet to find pN and pU, which express our "real" factor prices, w/pN and t/pU. This set of prices is exceedingly simple. We just multiply the expression for t/pU by our earlier expression for pN:
or, cancelling out t and (1-caLN):
which thus expresses the price of commodities as a function of the technological coefficients, c, aLU, aTU, aLN, aTN. Thus, relative prices are completely determined by technological conditions alone. We need not add any other components (notably, preferences/utility-based demand) into our analysis. But Richard Cantillon sought to reduce labor to land. In other words, he felt that labor should not be thought as contributing to value (i.e. prices) but rather only land. Labor, as we noted, was a technologically-produced "thing" dependent on necessities. As a result, the only "creator" of value, Cantillon held, was land. Land contributed to prices "directly" (through their own contributions to production) and "indirectly" (through creating the necessities necessary to sustain labor). As he writes:
How can we see this reduction of labor to land? Note that we have labor coefficients, aLU and aLN in our price equation but also note that these enter solely in the bracketed term in the denominator, (aLU/aTU - aLN/aTN). Now, these coefficient ratios are merely labor-land ratios, or factor intensity ratios: aLU/aTU is the "labor per unit of land" in producing luxuries and aLN/aTN is the "labor per unit of land" in producing necessities. We can alternatively think of these ratios as the "amount of land necessary to sustain labor". The greater the labor-intensity, the greater the amount of land "indirectly absorbed" (via labor) to produce goods. Note that if we have equal factor intensities in both sectors (aLU/aTU = aLN/aTN), then our price equation reduces to pN/pU = aTN/aTU, a pure land term. Note also that if luxuries are relatively more labor intensive, (i.e. aLU/aTU > aLN/aTN), then pN/pU < aU/aTN - or, in other words, the prices of luxuries are greater than necessities in terms of their direct land component because they have a greater "indirect" use of land (via labor). Similarly, if necessities are relatively more labor intensive, (i.e. aLU/aTU < aLN/aTN), then pN/pU > aTU/aTN, necessities are relatively more valuable than their pure land components indicate - again because of their greater indirect absorption of land. Thus, directly or indirectly, the relative amounts of land absorbed determine relative prices. We have reduced labor to land and thus we have a "land theory of value" - which Cantillon announced with his opening sentence: "The land is the source or matter from whence all wealth is produced." (Cantillon, 1755: p.2). So much for prices, but in a general equilibrium system, quantities must also be ascertained. In Cantillon's theory, these are easy to derive. Recall that we obtained the wage bill and rent bill equalities:
thus, using our previous expressions for w/pN and t/pU, we obtain:
Everything is alright for XU, but what about XN? We can reduce the first term further by recalling that L = LN + LU = aLNXN + aLUXU by the definition of total labor and technology. Thus plugging that into our first term:
which, rearranging, yields:
But we can now plug in our expression for XU:
cancelling terms:
Finally, multiplying our term for XU/T by T:
Et voilá! - we have the expressions for the "equilibrium" amounts of goods XN and XU produced. Again, note that they are functions solely of the technical coefficients and the amount of land in the economy, T. What about quantities of factors? Total land (T) was assumed fully employed by Cantillon. On the other hand, as we noted earlier, total labor (L) was presumed to be endogenous. The amount of labor employed can be easily calculated: namely, recall that L = aLNXN + aUXU, therefore all we need to do is to plug in the corresponding values of XN and XU we have just derived, i.e.
or simply:
which is labor employed - also a function of technical coefficients and the amount of land T. As we have seen, Cantillon had a fully-determined two-sector general equilibrium system; he had four markets, that of land, labor, luxuries and necessities and he could obtain four quantities and prices for them (where, naturally, all prices are "relative" prices, i.e. price ratios). The relative prices and relative quantities are determined by the relative absorption of land by the two goods, i.e. by the technical coefficients. The absolute quantities produced and the total level of employment vary directly with the total amount of land, T.
Selected References: H. Brems (1986) Pioneering Economic Theory, 1630-1980: A mathematical restatement, Baltimore: Johns Hopkins University Press. R. Cantillon (1755) Essay on the Nature of Commerce. H. Higgs translation, 1931, London: Macmillan. Friedrich A. Hayek (1936) "Richard Cantillon, sa vie, son oeuvre", Revue de Sciences Economiques, as translated and reprinted in Collected Works of F.A. Hayek, Vol. 3: The Trend of Economic Thinking: Essays on political economy and economic history. Chicago: University of Chicago Press. Antoin Murphy (1986) Richard Cantillon: Entrepreneur and economist. Oxford: Clarendon. G.L.S. Shackle (1982) "Cantillon Far Ahead of His Time", in Homenaje a Lucas Beltran. Madrid: Editorial Moneda y Crédito. Reprinted in S.F. Frowen, editor, Business, Time and Thought: Selected papers of G.L.S. Shackle. New York: New York University Press. J.A. Schumpeter (1954) History of Economic Analysis. New York: Oxford University Press. Joseph J. Spengler (1954) "Richard Cantillon: First of the moderns", Journal of Political Economy, Vol. 62, p.281-95, 406-24.
|
All rights reserved, Gonçalo L. Fonseca