The Edgeworthian Revival

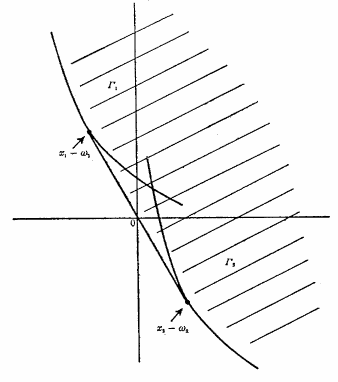
The Edgeworthian revival refers to the efforts to examine the relationship between a Walrasian competitive equilibrium and the solutions obtained via alternative exchange process (notably those from  game theory). The mathematical tools of choice that were introduced in this effort in the 1960s and 1970s -- i.e.  measure theory and non-standard analysis -- were substantially more demanding than anything most economists had been used to.

The central effort was the attempt to prove "Edgeworth's conjecture", i.e. that the core would shrink to the set of Walrasian Equilibrium if we increased the degree of competition (here formalized as the number of agents) to infinity.   In 1963, Gerard Debreu and Herbert E. Scarf set the ball rolling with their proof of core convergence within the context of a "replicated" economy (i.e. arbitrarily large numbers of agents of each type). In 1964, Robert Aumann proved the equivalence of the Edgeworthian core and the Walrasian equilibria when we have a continuum (uncountably infinite number) of agents.  This "new" definition of "perfect competition" required the introduction of measure theory -- notably Lyapunov's Theorem -- into economics. Edgeworth's conjecture in more general forms has been pursued by other economists since (esp. Truman Bewley (1973), Werner Hildenbrand (1974), Donald J. Brown and Abraham Robinson (1972, 1974), Robert M. Anderson (1978)).

The innovations continued.  New characterizations of competitive equilibrium were also achieved during this time.  We already know, from Aumann (1964) that competitive equilibrium can be characterized as a core with an infinite number of agents.    Later economists characterized equilibrium as limiting cases of other game-theoretic solution concepts, e.g. with the set of fair net trades by David Schmeidler and Karl Vind (1972), with the Shapley value  by Robert J. Aumann and Lloyd S. Shapley (1974), with the bargaining set by Andreu Mas-Colell (1989), for instance .   Unfortunately, these solution concepts are for "cooperative" games and, furthermore, require infinite number of agents.  Efforts have been made throughout , while we usually like to think that Walrasian equilibrium is non-cooperative and can be achieved with less than infinite number of agents. 

Top

The Founder Francis Ysidro Edgeworth, 1845-1926. Early Work on Edgeworthian Themes William Ernest Johnson, 1859-1931. Arthur L. Bowley, 1869-1957. Frederik Zeuthen, 1888-1959. Harold Hotelling, John Hicks, Abba Lerner and the Paretian Revival  John von Neumann, Oskar Morgenstern and Game Theory The Edgeworthian Revival Martin Shubik, 1926- Lloyd S. Shapley, 1923- Herbert E. Scarf, 1930- Gerard Debreu, 1921- Robert J. Aumann, 1930- Karl Vind, 1933- Werner Hildenbrand, 1936- David Schmeidler Truman F. Bewley, 1941- Donald J. Brown Abraham Robinson, 1918-1974. Andreu Mas-Colell, 1944- Hugo Sonnenschein M. Ali Khan Robert M. Anderson Brigit Grodal, 1934-2004

Top

Top

All rights reserved, Gonçalo L. Fonseca