When referring to the "stability" of equilibrium, or the dynamics which establish equilibrium, most Neoclassical economists immediately think of the Walrasian tâtonnement process. This is, far and away, the most popular form of adjustment. It is what is taught immediately when the theory of "demand-and-supply" is first encountered.

The pioneer Léon Walras (1874) was obsessed with stability, in particular, in providing the mathematical conditions that would ensure that prices will gravitate towards equilibrium. Is such a proof necessary? Hopefully, as the discussion earlier indicated, it is. To the common claim that stability is already self-evident in the concept of equilibrium itself, Walras was to respond that "Nothing is self-evident except axioms, and this is not an axiom." (Walras, 1874: p.470).

It is also important for practical reasons. The entire defense of laissez-faire as an economic policy rests on the assumption that markets are "stable" in the sense given above, otherwise the economy might not move towards its celebrated equilibrium on its own. As Walras notes again:

"Conversely, the fact that economists have often extended the principle of free competition beyond the limits of its true applicability is proof positive that the principle has not been demonstrated." (Walras, 1874: p.256-7)

Above everything, stability is theoretically important. The constant effort by economists to "solve" for the equilibrium of a system will turn out to be vacuous if that equilibrium is unstable, i.e. if there is no way of getting there, even theoretically. Walras was particularly insistent on this. As he argued:

"Now there remains to show -- and this is the essential point -- that the problem of exchange for which we have just given a theoretical solution is the selfsame problem that is solved empirically on the market by the mechanism of free competition." (Walras, 1874: p.162-3).

The "theoretical" problem Walras refers to in this passage is finding what the equilibrium is. For an economist, this is a matter of simple mathematics: when we have all demands and supplies laid out, it is straightforward enough to compute the equilibrium (although, in practice, that tends to be quite complicated). But how does "the market" find it? How does the market "move" the economy towards it? This is the "stability" question.

Walras conceived of the "mechanism of free competition" in a precise, but very familiar manner: the Law of Excess Demand. This "Law" claims that prices adjust in response to excess quantity demanded. So, if there is an excess demand for apples, the price of apples increases; if there is an excess supply of apples, the price of apples declines.

Mathematically, letting q^d(p) be the quantity of apples demanded and q^s(p) the quantity of apples supplied, then the Law of Excess Demand is simply:

dp/dt = ¦ [q^d(p) - q^s(p)]

where ¦ ¢ > 0, so:

if q^d(p) > q^s(p), then dp/dt > 0

if q^d(p) < q^s(p), then dp/dt < 0.

This law is depicted in Figure 1. If we begin at a price above equilibrium (e.g. p¢ ), then there is excess supply of that good, and thus its price will fall (from p¢ towards p*); if we begin at a price below equilibrium (e.g. p¢¢ ), then there is excess demand and its price will rise (from p¢¢ to p*).

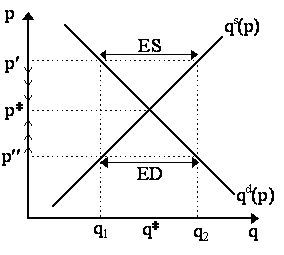
Fig. 1 - The Law of Excess Demand

Paul Samuelson (1941, 1947) has insisted that the "true dynamics" underlying the process must be clarified. In Figure 2, the familiar supply-and-demand diagram is depicted in the right quadrant, the price path over time, p(t), is depicted in the left quadrant. If the price of apples begins at p₀, the quantity demanded is q₀^d and the quantity supplied is q₀^s. There is excess supply in the market for apples, shown by the horizontal difference Z in Figure 2. As a result of this glut, the price begins to decline. As it falls, the quantity demanded of apples begins to increase and the quantity supplied will be reduced.

By time period t, price has gone down from p₀ to p₁, while the quantity demanded has increased from q₀^d to q₁^d and the quantity supplied decreased from q₀^s to q₁^s. However, p₁ is not good enough: there is still excess supply, so the price of apples will continue to fall below that. The price will only stop falling when it hits p*, as then the quantity demanded will be equal to the quantity supplied (q*). Thus, the price path p(t) converges to the equilibrium price p* as time goes on, i.e. p(t) ® p* as t ® ¥ .

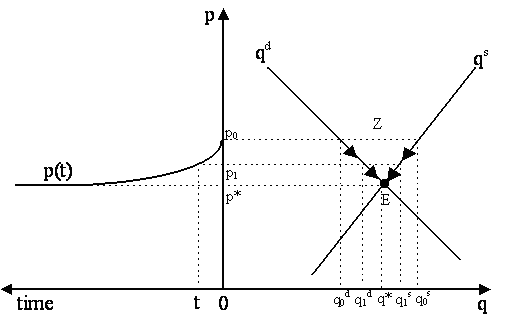
Fig. 2 - Walrasian Dynamics

There are important points not really clarified in this simple "Law". For instance, who does the adjusting of prices is not made clear. As Kenneth Arrow notes,

"Each individual participant in the economy is supposed to take prices as given and determine his choices as to purchases and sales accordingly; there is no left over whose job it is to make the decision on price." (Arrow, 1959: p.43).

Léon Walras did not really answer Arrow's question directly. Rather Walras went on to argue that we could conceive of a market with free competition as analogous to a situation where there is an independent central "crier" or "auctioneer" announcing prices which traders take as "given" and react accordingly with their demands and supplies.

Of course, this answer brings forth its own set of questions. Firstly, it is a simple fact that in most markets, this "auctioneer" does not exist. As explained by Kregel (1995), Walras's tâtonnement mechanism did have a "real world" counterpart in the operations of the 19th Century Paris Bourse (and, as Smith (1987) reminds us, in the modern London Gold Market). But these examples are few and far between. Extending the analogy to markets in general is by no means obvious.

Secondly, even if we did allow the tâtonnement analogy to be stretched, we still have not answered what are the underlying motivations and behavioral rules that make it work. As Tjalling Koopmans asks:

"If, for instance, the net rate of increase in price is assumed to be proportional to the excess of demand over supply, whose behavior is thereby expressed? And how is that behavior motivated? And is the alternative hypothesis, that the rate of increase in supply is proportional to the excess of demand price over supply price any more plausible, or any better traceable to behavior motivation?" (Koopmans, 1957: p.179)

Thirdly, pursuing the behavioral question further, if traders understand how the tâtonnement mechanism works, why do they reveal their true demands and supplies when the auctioneer makes his price announcement? A trader could act strategically, say, by holding back or falsely putting forth demands and supplies with the purpose of tricking the auctioneer into bringing down the prices for the goods the trader really wants and raising the prices of those goods he has to sell. Such manipulative behavior is not unknown in real markets. Yet Walras does not (really) discuss the market institutions that prevent strategic behavior.

Fourthly, even supposing that prices could be settled upon by such a mechanism, there is still nothing that implies that it is implementable in a decentralized manner, i.e. that there is a sequence of bilateral exchanges that would carry the equilibrium trades through. One would need the contrivance of money or some other institutional mechanism. But, if such details are introduced, would they not implicate "price-groping" phase as well? (cf. Starr, 1989; Ostroy and Starr, 1990).

A tremendous debate has also swirled around whether Walras  himself believed that trade between agents occurred before or only after equilibrium prices were reached by the auctioneer. In the "no-trade-before-equilibrium" version, the "auctioneer" yells out a random set of prices. Traders react to these prices with demands and supplies of various articles. What they present to the auctioneer are not the goods themselves, but "tickets" (or "bons") representing the quantities they wish to trade. If the quantities demanded match the quantities supplied in each market, then an equilibrium has been reached and, with auctioneer's assent, the agents can proceed to trade their articles. But if the quantities demanded and supplied do not match, then everything is cancelled and no trade occurs. The auctioneer must try again.

However, tickets were only introduced when Walras was discussing exchange in an economy with production (Walras, 1874: Leç. 20). In his discussion of stability in a pure exchange economy (Leç. 12), he did not use this artifact. This has led some commentators to argue, therefore, that at least his pure exchange process allowed for out-of-equilibrium trade -- what Hicks called trading at "false prices" (Hicks, 1939: p.128-9). For a flavor of the ensuing debate, see Goodwin (1951), Patinkin (1956), Morishima (1977), Jaffé (1967, 1981), Walker (1987, 1996) and Kompas (1992). Although the no-trade-before-equilibrium version of the story has dominated the modern discussion of stability in a Walrasian system, a small tradition of what are called non-tâtonnement mechanisms has pursued stability with out-of-equilibrium trade.

The time has come to begin making Walras's stability theory a bit more mathematically precise. Assuming that the Walrasian tâtonnement is the one and only adjustment mechanism in operation, does it actually yield stability? Does an auctioneer, groping around according to the Law of Excess Demand, eventually approach equilibrium?

Léon Walras (1874) did not demonstrate this "properly", i.e. with the mathematics of dynamical systems, but only intuitively. Most of his successors, such as Antonelli, Pareto, etc., failed or did not even attempt to prove it either. The first concrete step in the right direction was John Hicks (1939). The "true" dynamic conditions, in terms of differential equations, were only established later by Paul Samuelson (1941, 1942, 1947), Lloyd Metzler (1945), Kenneth Arrow, H.D. Block and Leonid Hurwicz (1959), Lionel McKenzie (1960) and others.

As this literature on both local stability and global stability in a multi-market scenario is quite complex, we review it separately. For the moment, it suffices perhaps to follow a simple demonstration, in a single market. Samuelson's (1941, 1947) "true" dynamics of differential equations can make the intuition we have pursued thus far more precise. In a single market, let us have linear demand and supply curves:

q^d(p) = a₀ + ap

q^s(p) = b₀ + bp

where a < 0 and b > 0, naturally, so the demand curve is downward-sloping and the supply-curve is upward-sloping. Equilibrium price p* is defined where:

q^d(p*) = q^s(p*)

and this can be solved for our simple linear equations quite simply as:

p* = (a₀ - b₀)/(b - a)

As (b - a) > 0 by assumption, then for p* to be positive, it must also be that a₀ > b₀ (i.e. horizontal demand intercept is greater than the horizontal supply intercept). Now let the Walras tâtonnement process, the Law of Excess Demand, be defined as a differential equation so:

dp/dt = k[q^d(p) - q^s(p)]

where k (a "speed of adjustment" parameter) is assumed positive. Thus, this equation relates price changes to excess demand in the market like Walras proposed. Plugging in our equations for demand and supply, we obtain:

dp/dt + (b - a)kp = k[a₀ - b₀]

which is a simple first order linear differential equation. The particular integral (i.e. setting dp/dt = 0 and solving for p) is actually our equilibrium price, p* = (a₀ - b₀)/(b - a). The complementary function is simply (p* - p(0))e^-k(b-a)t where p(0) is the initial price, p* the equilibrium price (thus (p* - p(0)) expresses how far we are away from the equilibrium) and e is the natural base. Thus, the solution to the differential equation (the dynamic path of p) is merely:

p(t) = (p* - p(0))e^-k(b-a)t + p*

Now, the market is "stable" if p(t) approaches p* over time, i.e. p(t) ® p* as t ® ¥ . For this to be true, it must be that the entire expression subscripted above the natural base is negative. We know k and t are positive, thus for -k(b-a)t < 0, it must be that (b-a) is also positive. But to say that b > a, or equivalently, in terms of slopes, 1/b < 1/a. If our demand-and-supply curves take the "normal" shape we drew them in, then a < 0 and b > 0 and thus the condition is met. If both curves sloped upwards, so b, a > 0, then the demand curve must be steeper than supply; if both slope downwards, so b, a < 0, then the supply curve must be steeper.